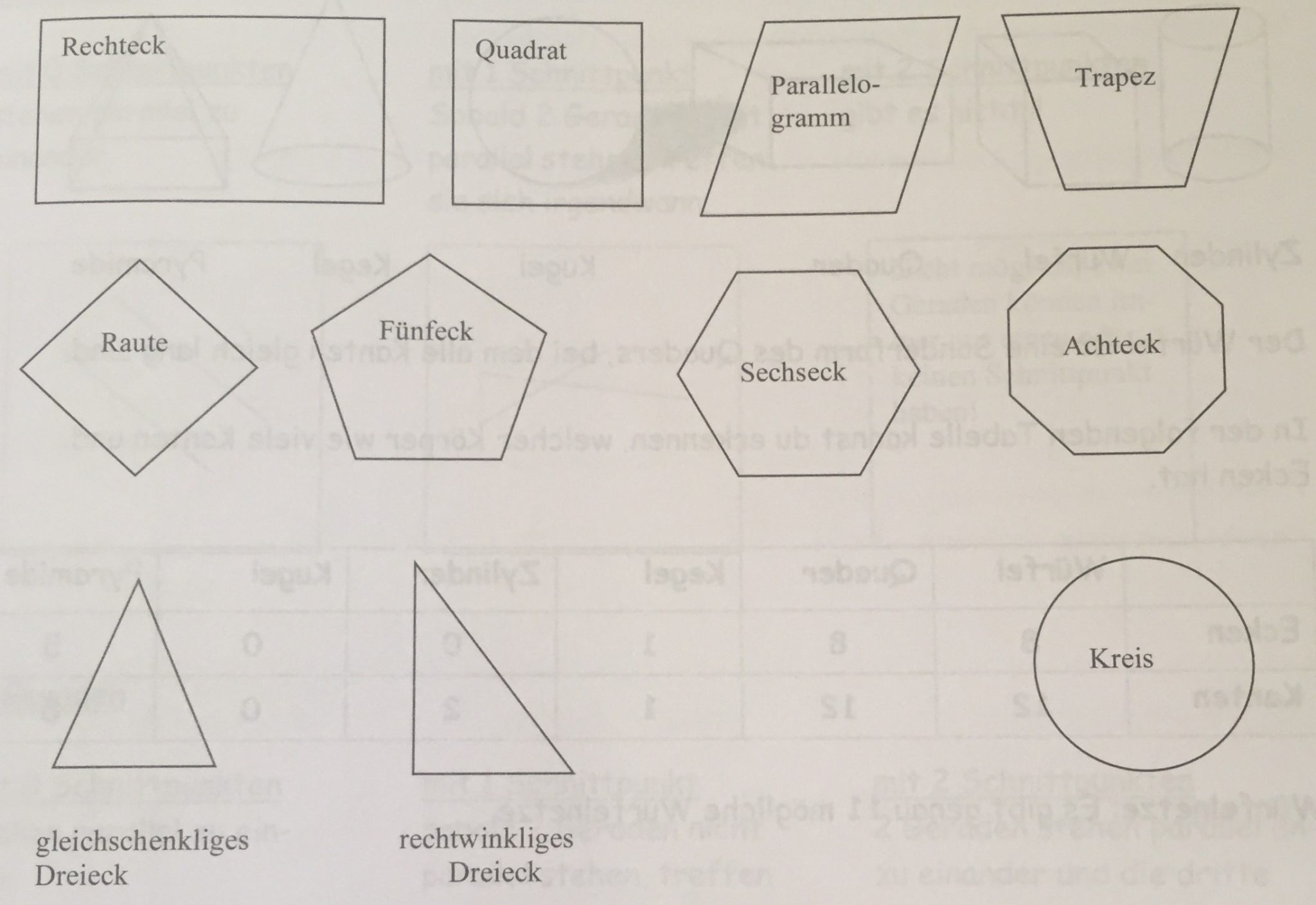
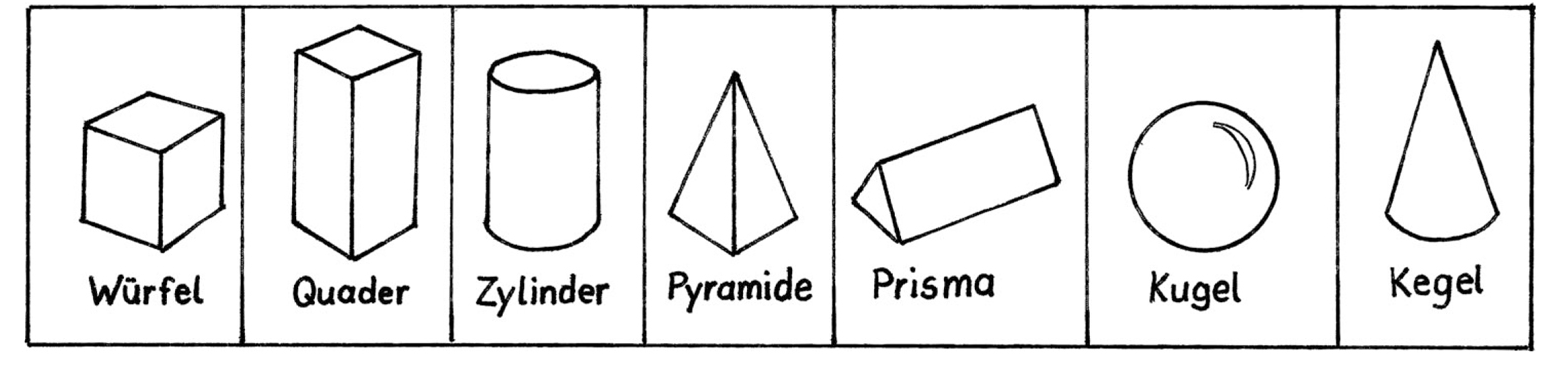
Flächen sind zweidimensional (2D), also ganz flach. In Körper könnte man etwas hineinfüllen, sie sind dreidimensional (3D).
Verschiedene Flächen siehst du auf diesem Bild:
Verschiedene Körper siehst du auf diesem Bild:
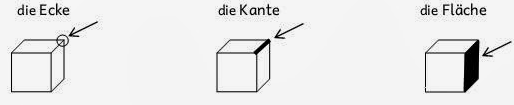
Diese Körper haben unterschiedlich viele Ecken, Kanten und Flächen. Hier sind die Begriffe erklärt:
Ein Würfel hat zum Beispiel 8 Ecken, 12 Kanten und 6 Flächen. Überlege kurz, wie die Lösung für einen Kegel ist… (Lösung: 2 Flächen, 1 Kante und 1 Ecke (Spitze))
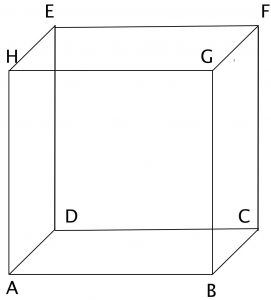
Kantenmodell
Bei einem Kantenmodell wirkt es ein bisschen so, als könnte man durch den Würfel durchschauen. Als wäre er durchsichtig. Daher kann man auch die Kanten, Flächen und Ecken sehen, die man sonst vielleicht nicht sieht. (Das nennt man auch: Glaskörper)
An einem solchen Kantenmodell könnte man entlanglaufen. Wenn bei dem Bild eine Spinne an der Ecke A sitzt, auf welchem Weg könnte sie dann zu einer Fliege an Ecke F kommen? Sie darf nur auf den Kanten laufen…
Würfelnetze
Sechs zusammenhängende Quadratflächen, die so angeordnet sind, dass sie sich zu einem Würfel zusammenfalten lassen, werden als Würfelnetze bezeichnet. Wenn du einen Würfel aus Papier so an den Kanten aufschneidest, dass am Ende immer noch alle Teile zusammenhängen, dann erhältst du ein Würfelnetz.
Du könntest auch einen Würfel auf einem Blatt Papier abrollen und die Flächen abzeichnen. Dadurch findest du aber nicht alle Würfelnetze. Im Video wird dir das hier erklärt.
Es gibt insgesamt 11 Möglichkeiten, wie ein Würfelnetz aufgebaut sein kann. Eine Übersicht gibt es hier.
In diesem Video erklärt eine Schülerin, wie man Würfelnetze erkennt: youtube.com
weiteres Material zum Üben gibt es hier: pikas.de, matheaufgaben.net,
Quadernetze
Auch ein an den Kanten aufgeschnittener Quader ergibt ein Quadernetz. Bei einem Würfel sind alle Flächen gleich groß, aber beim Quader erhält man durch die rechteckigen Flächen viel mehr verschiedene Würfelnetze.
Wenn alle drei gegenüberliegende Flächen (oben und unten, links und rechts, hinten und vorne) unterschiedlich groß sind, erhältst du 54 verschiedene Quadernetze. Eine vollständige Übersicht findest du hier.
Ansichten
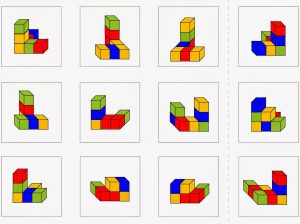
Aus mehreren Würfeln kann man auch Würfelgebäude bauen. Diese könnten zum Beispiel so ausschauen:
Wenn man jetzt diese Würfelgebäude genau von vorne anschaut (oder von hinten, von links, von rechts, von oben) dann erhält man Ansichten von diesen Würfelgebäuden.
Ein Erklärvideo dazu kommt noch!
Bauplan
Von diesen Würfelgebäuden kann man auch einen Bauplan erstellen. Wenn ein anderes Kind diesen Bauplan bekommt, dann kann es das Würfelgebäude nachbauen!!
Ein Erklärvideo dazu kommt noch!
Hier siehst du, wie Lars, Max und Luisa dir erklären, wie man ohne Zirkel einen Kreis zeichnen kann:
Vom Cornelsen-Verlag gibt es auch ein Erklärvideo zur Geometrie: